le blog déménage

La suite du blog est ici désormais.

SEND+MORE=MONEY

petit exercice au stage de python au CIRM (*):

trouver à l'aide d'un programme python comment remplacer chaque lettre par un chiffre différent pour que l'addition suivante soit juste:

   SEND
+  MORE
-------
= MONEY

bien sûr, S et M ne sont pas remplacés par 0

Une solution en python:


def verif(s,e,n,d,m,o,r,y):
    if s != 0 and m != 0 and (d+n*10+e*100+s*1000)+(e+r*10+o*100+m*1000) == y+e*10+n*100+o*1000+m*10000:
        return True
    else: return False
   
sol = []

def choix_ordonne(l1,p,l):
    global sol
    if p==0:
        if verif(*l1): 
            sol += [l1]
            print(l1)
    elif l==[]: pass
    else: 
        for x in l:
            l2 = [y for y in l if y != x]
            choix_ordonne(l1+[x], p-1,l2)
        
verif(1,2,3,4,5,6,7,8)

choix_ordonne([],8,[0,1,2,3,4,5,6,7,8,9])

print(str(len(sol))+' solution'+ ('' if len(sol)<2 else 's')+':')
for s in sol:
    print(s)

PS: la fonction choix_ordonne(l1,p,l) énumère tous les choix possibles de p éléments pris dans la liste l, et teste s'ils vérifient la fonction verif lorsqu'ils sont ajoutés à la fin de la liste l1. Ceux qui la vérifient sont ajoutés à la liste globale sol.

(*) j'ai appris plein de choses sur python pendant ces 3 jours, merci en particulier à Marc, Judicaël, Benjamin et Luc!

diagonalisation d'une matrice

Avec numpy:

>>> from numpy import *

on donne une matrice $3\times 3$ ligne par ligne :


>>> A = matrix([[1,2,3],[4,5,6],[7,8,1]])

>>> A
matrix([[1, 2, 3],
        [4, 5, 6],
        [7, 8, 1]])


le tableau de ses valeurs propres :
>>> eigvals(A)
array([ 12.45416474,  -0.37976219,  -5.07440255])

$3$ racines réelles simples, $A$ est donc diagonalisable, voici ses valeurs propres suivies de la matrice de passage dans la base des vecteurs propres :
>>> eig(A)
(array([ 12.45416474,  -0.37976219,  -5.07440255]), matrix([[-0.29373774, -0.73967882, -0.29720654],
        [-0.69005397,  0.66500848, -0.39870229],
        [-0.66147083, -0.10314536,  0.86758559]]))
>>> P=eig(A)[1]

on construit une matrice diagonale à partir du tableau des valeurs propres :
>>> D=diag(eig(A)[0])

et on vérifie que $A = P D P^{-1}$
>>> A-P*D*inv(P)
matrix([[ -2.22044605e-15,  -1.33226763e-15,  -4.44089210e-16],
        [ -1.77635684e-15,   0.00000000e+00,   1.77635684e-15],
        [ -4.44089210e-15,  -5.32907052e-15,  -2.66453526e-15]])

comme mumpy fait des calculs approchés, le résultat n'est pas exactement $0$, mais pas loin...

calcul approché de $\pi$ avec la moyenne arithmético-géométrique

Suivant un vieux sujet du CAPES (1995), voici programmé en python (avec sympy) un algorithme inspiré de [Salamin 1976]:


from sympy import *
import sympy as sp

x = sp.symbols('x')

def fu(n,x):
    if n==0: return x
    else: return (fu(n-1,x)+fv(n-1,x))/2

def fv(n,x):
    if n==0: return 1
    else: return sqrt(fu(n-1,x)*fv(n-1,x))

def fy(n,y):
    return (fu(n,x)/fv(n,x)).subs(x,y)
    
def fz(n,y):
    return (diff(fv(n,x),x)/diff(fu(n,x),x)).subs(x,y)
    
def fpi(n):
    if n==0: return (2+sqrt(2))
    else: return fpi(n-1) * (1 + fy(n,1/sqrt(2))) / (1 + fz(n,1/sqrt(2)))
    
for n in range(10): 
    p = 1000
    print('n='+ str(n) 
          + ': erreur 10**('
          + str(N(ln(N(fpi(n)-pi,p))/ln(10),5)) 
          + ')')

en faisant les calculs approchés avec $1000$ chiffres significatifs, l'exécution de ce code donne $\pi$ avec 700 décimales au bout de seulement 8 étapes (la précision double à chaque étape, en fait):

n=0: erreur 10**(-0.56444)
n=1: erreur 10**(-2.9939)
n=2: erreur 10**(-8.1322)
n=3: erreur 10**(-18.737)
n=4: erreur 10**(-40.262)
n=5: erreur 10**(-83.619)
n=6: erreur 10**(-170.64)
n=7: erreur 10**(-344.98)
n=8: erreur 10**(-693.95)

quelques algorithmes qui pourraient bien être au programme des CPGE l'an prochain

Programmation en python d'algorithmes simples et utiles.
(le fichier est ici: algos_au_programme.py)

1. recherche dans une liste

def recherche_dans_liste(x,l):
    for k in range(len(l)):
        if x == l[k]: return(True)
    return(False)

        (aparté pour les informaticiens:

        # pour tester agréablement les fonctions lorsqu'on

        # exécute le fichier dans python(x,y) par exemple 

        # test(f,a1,...,an) affiche le résultat de f(a1_,...,an)

        # précédé du nom de f et de ses arguments 

        import re

        def test(f,*args):

            s = str(f)

            nomf = re.split(' ',s)[1]

            print(nomf, args)

            print('donne: '+ str(f(*args)))

        fin de l'aparté)

# testons la fonction recherche_dans_liste
test(recherche_dans_liste,'charlie',[4,2,'charlie',6])
# on note au passage que les listes de python ne sont pas homogènes
test(recherche_dans_liste,0,[2,1,2,3])

2. recherche du maximum dans une liste de nombres

def maximum_liste(l):
    m = None # j'avais mis -sys.maxint, Marc a mieux
    for x in l: m = max(m,x)
    return(m)
    
test(maximum_liste,[3,5,0,4])
test(maximum_liste,[])

3. calcul de la moyenne et de la variance.

def moyenne_liste(l):
    return(sum(l)/len(l))
    
Si $l=[x_1,\ldots,x_n]$, la variance de $l$ est $\sigma^2=\cfrac 1 n \sum_{i=1}^n (x_i - x)^2$, avec $x=\cfrac 1 n \sum_{i=1}^n x_i$ la moyenne de $l$ (révisons pour l'année prochaine...:)).

def variance_liste(l):
    m = moyenne_liste(l)
    return(sum([(x-m)**2 for x in l])/len(l))
    
test(moyenne_liste,[1,2,3,4,5])
test(variance_liste,[1,2,3,4,5])

3. recherche par dichotomie dans un tableau trié.
On va dire que tableau = liste
Rend i tel que t[i] = x

def recherche_dans_tableau_trie(x,t):
    if len(t) == 0: return(None)
    a = 0
    b = len(t)-1
    while a <= b: 
        c = int((a+b)/2)
        if x == t[c]: return(c)
        elif x < t[c]: b = c - 1
        else: a = c + 1
    return None
    
test(recherche_dans_tableau_trie,2,[0,1,2,3,4])
test(recherche_dans_tableau_trie,2,[0,1,3,4])
test(recherche_dans_tableau_trie,2,[])

4. recherche par dichotomie du zéro d’une fonction continue et monotone.
f est la fonction, [a,b] est l'intervalle de recherche
et p est la précision: on s'arrête quand b-a < 10^(-p)

def recherche_zero_dichotomie(f,a,b,p):
    precision = 10**(-p)
    if f(a)*f(b) > 0: return(None)
    while b-a > precision: 
        c = (a+b)/2.
        if f(a)*f(c) > 0: a = c 
        else: b = c
    return(a) 

# en python, la fonction x |---> 1-x s'écrit lambda(x): 1-x
test(recherche_zero_dichotomie,lambda(x): 1-x,0,2,5)
test(recherche_zero_dichotomie,lambda(x): log(x)-1,1,3,10)

5. méthodes des rectangles et des trapèzes pour le calcul approché d’une intégrale sur un segment.
La précision est la largeur maximale des rectangles: 10^(-p)

def integrale_approchee_rectangle(f,a,b,p):
    dx = 10.**(-p)
    n = int((b-a)/dx)
    aire = 0.
    k = 0
    while k < n: # on aurait pu utiliser un for mais le range aurait pu
                 # être trop gros et faire planter le système ...
        aire = aire + f(a+k*dx)*dx
        k = k+1
    return(aire)
    
test(integrale_approchee_rectangle,lambda x: x,0,1,5) 
# calcul de Pi
test(integrale_approchee_rectangle,lambda x: 4/(1+x**2),0,1,6) 

def integrale_approchee_trapeze(f,a,b,p):
    dx = 10.**(-p)
    n = int((b-a)/dx)
    aire = 0.
    k = 0
    while k < n: 
        ak = a+k*dx
        aire = aire + (f(ak)+f(ak+dx))/2*dx
        k = k+1
    return(aire)
    
test(integrale_approchee_trapeze,lambda x: x,0,1,5) 
# calcul de Pi, bien meilleur qu'avec les rectangles
test(integrale_approchee_trapeze,lambda x: 4/(1+x**2),0,1,6) 

6. recherche d’un mot dans une chaîne de caractères.
Rend le rang dans la chaîne où commence le mot m s'il existe, sinon rend None

def recherche_mot(m,s):
    p = len(m)
    n = len(s)
    for k in range(n-p+1):
        i = 0
        while i < p:
            if m[i] != s[k+i]: i = p
            elif i == p-1: return(k)
            else: i = i+1
    return(None)

test(recherche_mot,'ab',' ab')
test(recherche_mot,'charlie','ou est charlie dans cette phrase?')

test(recherche_mot,'charline','ou est charlie dans cette phrase?')

polynômes de Hermite: calcul avec sympy et tracé avec matplotlib

Avec
$$\phi(x)=e^{-\cfrac {x^2} 2}$$
 on pose
 $$P_n(x)=\cfrac {(-1)^n} {n!} e^{\cfrac {x^2} 2} \phi^{(n)} (x)$$

pour calculer facilement ces polynômes, si l'on n'a pas l'expression de leurs coefficients, on peut dériver plusieurs fois formellement, et sympy s'impose:

from sympy import symbols, diff, exp, factorial, simplify, expand
import sympy as sp

def phi(x):
  return(exp(-x**2/2))

X = sp.symbols('X')

def hermite(n):
  P = (-1)**n/factorial(n)*exp(X**2/2)*diff(phi(X),X,n)
  return(expand(simplify(P)))


on obtient par exemple:

print([(n,hermite(n)) for n in range(5)])
>>> [(0, 1), (1, X), (2, X**2/2 - 1/2), (3, X**3/6 - X/2), (4, X**4/24 - X**2/4 + 1/8)]

d'où
$$P_4 = \cfrac {X^4} {24} - \cfrac {X^2} 4 + \cfrac 1 8$$

 Pour le tracé, utilisons matplotlib, plus souple (*).

Le code python est ici: polynomes_hermite.py
Le tracé:

Note: si on veut faire cohabiter sans problème sympy et matplotlib, il faut les importer avec précautions, pas tout d'un bloc:

from sympy import symbols, diff, exp, factorial, simplify, expand
import sympy as sp

import numpy as numpy
import matplotlib.pyplot as pyplot

(*) par exemple, je ne sais toujours pas ajouter des textes dans les graphiques tracés avec le plot de sympy (à part le titre du graphique).

la méthode de Newton, avec sympy

On se sert de sympy pour dériver formellement une fonction python, et utiliser la dérivée dans la méthode de Newton. Le code, fondé sur celui d'un lecteur anonyme, est ici: newton.py
Le graphique associé, avec matplotlib:

courbes paramétrées avec Python(x,y) et matplotlib

Deux courbes paramétrées: ellipse et cardioïde (déformée), comme exemples de bords de parties convexes ou non du plan:

le code python est ici: partie_convexe.py

développements limités, graphiques avec sympy

Des développements limités avec sympy (le code python est ici).

Les fonctions rencontrées dans la suite:
series
limit
subs (plus un peu de programmation objet)
factor
solve
plot

1. Calculs

Allons-y (dans Python(x,y) par exemple)

from sympy import *
x, y, z, t = symbols('x y z t')

# la fonction à utiliser pour calculer un développement limité en sympy
# est series:
series(exp(x),x,0,10)

# comme sympy utilise $O(x^n)$ au lieu de $o(x^n)$ dans les développements
# limités, ajouter 1 à l'ordre usuel
# pour un DL de $e^x$ en 0 à l'ordre 3:
series(exp(x),x,0,4)

# mais python est un langage de programmation, on peut écrire une
# fonction convenable:
def DL(f,v,a,n):
   return (series(f,v,a,n+1))

# quelques exemples
series((sin(x)-x)/x**3, x, 0, 3)
DL((sin(x)-x)/x**3, x, 0, 2)
# on en déduit la limite:
limit((sin(x)-x)/x**3, x, 0)

# DL de $\sqrt{1+x^3}$ à l'ordre 6 en 0
DL(sqrt(1+x**3), x, 0, 6)

# DL de $\tan$ en 0 à l'ordre 5
dl=DL(tan(x), x, 0, 5)
print(dl)

Transformons le développement limité en polynôme en éliminant le $O(x^6)$.
Pour cela on utilise la programmation objet de python: l'objet dl possède une fonction propre à sa classe (comme une classe sociale ou une classe de lycée) qui s'appelle subs: on l'utilise sans donner l'objet dl en paramètre puisqu'elle le connaît déjà. Ce genre de fonction de classe s'appelle méthode.

p=dl.subs(O(x**6),0)
print(p)

# factorisons p
p1=factor(p)
print(p1)

#cherchons les racines de p1
sols=solve(p1,x)
print('polynome de degre '+str(p1.as_poly().degree())
      + ', '+str(len(sols))+ ' racines trouvees',
      sols)

# un DL nul en 0+
DL(exp(-1/x), x, 0, 3)
# en effet la limite suivante est nulle:
limit(exp(-1/x), x, 0, dir="+")

2. Graphiques

On va utiliser le module de tracé de courbes de sympy (documentation ici), qui permet de tracer des fonctions données par des expressions formelles, ce que matplotlib ne sait pas faire:


from sympy import *
x, y, z, t = symbols('x y z t')

La fonction de tracé de sympy s'appelle simplement plot,
elle rend en argument la fonction, puis un triplet qui indique la variable de la fonction et ses bornes de variation:

plot(sin(x), (x,-4*pi,4*pi), title='$\$$\sin(x)$\$$')

donne

on peut faire des tracés multiples, il suffit de mettre à la suite les fonctions. Ici $\sin$ et son développement limité à l'ordre 3:

plot(sin(x), series(sin(x),x,0,4).subs(O(x**4),0), (x,-pi,pi),
     title='$\$$\sin(x)$\$$ et son DL en 0 a l\'ordre 3')

donne

même chose à l'ordre 5:

plot(sin(x), series(sin(x),x,0,6).subs(O(x**6),0), (x,-pi,pi),
     title='$\$$\sin(x)$\$$ et son DL en 0 a l\'ordre 5')

donne

enfin avec plus de DL, où on voit bien l'approximation:

plot(sin(x),
     *[series(sin(x),x,0,2*n).subs(O(x**(2*n)),0) for n in
     range(1,5)]
     +[(x,-pi,pi)],
     title='$\$$\sin(x)$\$$ et ses developpements limites en 0
     aux ordres $1,3,5,7,9$')

donne

Je ne sais pas encore mettre des couleurs différentes aux courbes...

graphiques avec Python(x,y) et matplotlib: suite

Le théorème des accroissements finis:

- le code python à charger dans Python(x,y) et à exécuter: accroissements_finis.py (un peu commenté).
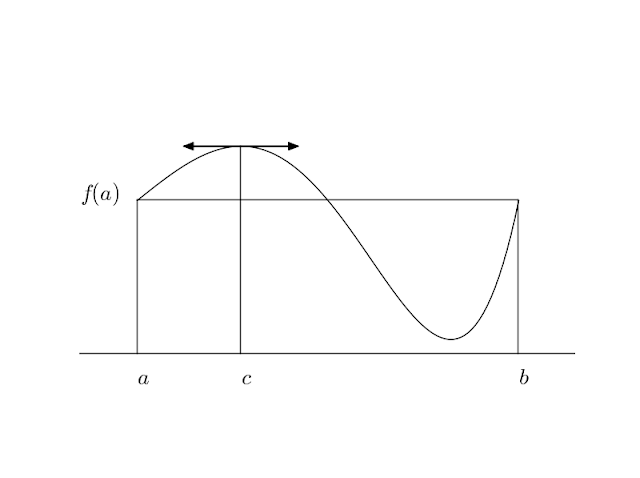
pour éviter de répéter des commandes matplotlib longues, j'ai programmé quelques petites fonctions: tracé d'un segment, d'une flèche, d'une double flèche de tangente, d'un texte. C'est un avantage de python par rapport à tikz où la programmation est fastidieuse (du moins le peu que j'en ai fait). J'utilise solve de sympy (calcul formel) pour trouver c tel que $f'(c)=\cfrac {f(b)-f(a)}{b-a}$.

- le schéma que cela donne:

graphiques avec Python(x,y) et matplotlib

matplotlib est intégré à Python(x,y), pas besoin de le télécharger.
C'est un ensemble de fonctions qui permettent de tracer des graphiques mathématiques.
La liste des fonctions et leur documentation est là (en anglais...)

1. Un premier essai: tracer la fonction sinus sur $[0,6\pi]$:

on charge les bibliothèques nécessaires:


from math import *
import numpy as numpy
import matplotlib.pyplot as pyplot

une courbe est une suite de points du plan reliés par des segments: s'il y en a beaucoup, on a l'illusion d'une courbe lisse.

on crée d'abord la liste t des abcisses de 100 points régulièrement répartis dans $[0,6\pi]$: 

t = numpy.linspace(0.,6*pi,100)

puis on trace la courbe en donnant la liste des ordonnées correspondant aux abcisses données dans la liste t:

pyplot.plot(t, [sin(x) for x in t],'k')

ensuite on définit les bornes du tracé:

pyplot.axis([0,6*pi,-1.5,1.5])

on trace l'axe des abcisses en noir:

pyplot.axhline(linewidth=1, color='k')

puis on insère la définition de la fonction au point $(2,1)$ du plan:

pyplot.text(2,1, r'$\$$x\mapsto\sin(x)$\$$', color='k')

finalement s'affiche cette fenêtre (si elle n'apparaît pas, c'est peut-être qu'elle se trouve cachée derrière une fenêtre, alors cliquer sur son icône dans la barre des tâches):

on peut enregistrer le graphique sous forme d'une image en cliquant sur l'icône en disquette, cela donne cette image:

Notez la possibilité d'écrire du Latex dans les textes du graphique, la classe!

2. Le théorème de Rolle:


# théorème de Rolle
from math import *
import numpy as numpy
import matplotlib.pyplot as pyplot

# les bornes des intervalles
a=0.5
b=2.5
a1=a-0.3
b1=b+0.3
h=4
# la fonction dérivable en question
def f(x):
  y=x-0.5
  return(0.5*(y**5-5*y**3+4*y)+2)

# la courbe de la fonction
t = numpy.linspace(a,b,100)
pyplot.plot(t, [f(x) for x in t],'k')

# le rectangle englobant le tracé
pyplot.axis([a1,b1,-1,h])
pyplot.axis('off') # pour virer le cadre pas très joli
pyplot.plot([a1,b1],[0,0],color='k')
pyplot.plot([a,b],[f(a),f(b)],color='k')
pyplot.plot([a,a],[0,f(a)],color='k')
pyplot.plot([b,b],[0,f(b)],color='k')

c1=.5439122558+0.5 # le point où la dérivée s'annule
pyplot.plot([c1,c1],[0,f(c1)],color='k')

# pour tracer la tangente en (c,f(c)) et ses flèches,
# pas très élégant
pyplot.arrow(c1-0.3,f(c1),2*0.3,0,
  shape='full',head_width=0.1,head_length=.05,fc='k',
  length_includes_head=True)
pyplot.arrow(c1+0.3,f(c1),-2*0.3,0,
  shape='full',head_width=0.1,head_length=.05,fc='k',
  length_includes_head=True)

# enfin les textes du schéma
pyplot.text(a,-0.4, r'$a$', color='k', size=20)
pyplot.text(b,-0.4, r'$b$', color='k', size=20)
pyplot.text(a-0.3,f(a), r'$f(a)$', color='k', size=20)
pyplot.text(c1,-0.4, r'$c$', color='k', size=20)

# sauvegarde le schéma dans un fichier
savefig('rolle.png',format='png')

donne cette image, une fois sauvegardé dans le fichier:

je crois bien que je vais laisser tomber tikz... :)

python facile sous Windows: Python(x,y)

Python(x,y), c'est python à la portée de tout le monde sous Windows.
Voici comment débuter facilement. Pour la suite, consulter ce guide par exemple.

1.Télécharger Python(x,y) ici (patience, ça fait 500 Mégas mais ça vaut le coup),
puis l'installer, en  exécutant le fichier Python(x,y)-2.7.3.1.exe (re-patience, c'est longuet, mais ... je l'ai déjà dit.)
Si on veut faire du calcul formel (genre Maple), il faut ajouter sympy à Python(x,y).
Pour cela télécharger le fichier sympy-0.7.2-1_py27.exe ici, puis l'exécuter.


2. Ensuite, lancer Python(x,y) (raccourci du bureau, ou menu démarrer-> Python(x,y)->Python(x,y))
Dans la fenêtre qui s'ouvre, cliquer sur le carré avec la toile d'araignée, en face de Spyder/Options...:

Ça lance l'interface Spyder (je l'ai un peu réduite pour que ça ne soit pas trop large):

Bon, à gauche, il y a une fenêtre appelée Éditeur: 

c'est un éditeur de fichier, on y écrit ses programmes, on les sauvegarde, charge, l'édition classique d'un fichier genre Openoffice ou Word.

À droite, en bas, la fenêtre appelée  Console est une fenêtre d'exécution, où on tape des commandes et Python les exécute, en affichant le résultat.

3. Un premier programme: la fonction factorielle.

Tapons dans l'Éditeur, sur la dernière ligne (la ligne 8):

def fact(n):
    if n==0: return(1)
    else: return(n*fact(n-1))

attention aux décalages en début de lignes, il sont importants pour python.

Testons ce programme, pour cela on l'exécute avec la touche F5,
comme c'est un nouveau programme, cela ouvre une fenêtre de sauvegarde classique (cliquer sur l'image pour zoomer):

on sauvegarde donc notre programme dans un fichier,
ensuite, python demande comment exécuter:

 cocher <<Exécuter dans l'interpréteur Python ou IPython actif>>, puis cliquer Exécuter,
(ces deux étapes n'arriveront plus ensuite, python se souviendra de nos choix pour ce fichier)

et on voit que python l'exécute dans la fenêtre Console, en bas à droite:

Python connaît donc maintenant la fonction fact que l'on vient de programmer, testons-la en tapant
 fact(3) puis Entrée dans la fenêtre Console, sur la dernière ligne non vide (!):

On obtient la réponse souhaitée :)
Testons fact(100):

Pas mal ;)

Voilà, avec ça on peut déjà programmer et tester confortablement avec python.

4. Calcul formel:
il suffit de charger sympy dans la console:
from sympy import *
et voilà. Définissons, toujours dans la console,
quelques symboles utiles:
x, y, z, t = symbols('x y z t')
k, m, n = symbols('k m n', integer=True)
f, g, h = symbols('f g h', cls=Function)
et testons:

Cool.

utiliser sympy sous windows

sympy est le module de calcul formel de python, très proche de Maple.
Voilà comment l'installer sous windows 7 (sous vista sans doute aussi).

1. on se contente de python 2.

Là c'est facile, il y a tout un environnement de programmation avec édition de fichiers de programmes, gestion de projets, environnement d'exécution, tout pour l'utilisateur néophyte.
Voir le message suivant.

2. on veut python 3.

Deux solutions:

a) avec cygwin.

On installe cygwin, et du coup on travaille comme sous linux (emacs, xterm, etc).
C'est ce que je fais, mais il faut être un peu informaticien.

b) on n'y connaît rien à linux.

Là, c'est plus spartiate:

- installer python 3:

télécharger http://www.python.org/ftp/python/3.3.0/python-3.3.0.msi
exécuter ce fichier, cela installe python 3.3.0, par défaut dans C:\Python33

- copier sympy:

décompresser ce fichier: sympy-0.7.2.zip
  et mettre le répertoire sympy-0.7.2 qu'il contient dans C:\Python33
télécharger ce fichier: sympy.bat et le mettre dans C:\Python33

Pour lancer sympy, double-cliquer sur C:\Python33\sympy.bat

on a une console pas très jolie, dans laquelle on navigue sur la ligne de commande avec les flèches <- et ->, et dans les commandes précédentes avec les flèches haut et bas. On copie/colle avec le click droit dans la fenêtre. On peut changer les couleurs de la console (texte, foncd) en cliquant droit sur le haut de la fenêtre et en réglant les propriétés.

- exemples de commandes:

expand((x+y)**5)


factor(x**5-y**5)

limit(1/x, x, oo)

solve(x**3 + 2*x + 3, x)

diff(x**2-1,x)

diff(x**2-1,x,2)

integrate(1/x**2,x)

series(sin(x),x,0,5)

series(ln(1+x),x,0,5)

summation(1/2**n, (n, 0, oo))

factor(summation(k, (k, 0, n)))


groebner([x**2 + 1, y**4*x + x**3], x, y, order='lex') #grevlex

leçon 2: polynômes à une indéterminée

Le fichier de ce qui suit est ici. 
Marc m'a déjà corrigé ma copie là :)

# Polynômes à une indéterminée: \( \mathbb{R} [X] \) 

# 1. Représentation des polynômes
# on représente le polynôme \(a_nX^n+...a_1X+a_0\) par la liste de ses
# coefficients jusqu'à un certain degré, étant entendu qu'après ce degré
# les coefficients sont nuls
# on les ordonne par degré croissant:
# \([a_0,a_1,...,a_n]\)
# par exemple, soit p1 le polynôme \(2X^2-3X+1\)

# en python une liste est une suite d'éléments entre crochets,
# séparés par des virgules
p1=[1,-3,0,2]   # le polynôme 2X^3-3X+1
p2=[1,-3,0,2,0] # le même polynôme
p3=[1,3,5]      # le polynôme 5X^2+3X+1

# p1 et p2 représentent le même polynôme, mais pour python ce sont des listes différentes.

# quelques fonctions utiles sur les listes:
# range(n) produit la liste des entiers de 0 à n-1: [0,1,2,...,n-1]
# len(s) donne la longueur d'une liste s
# + concatène deux listes

# on accède à l'élément de rang k de la liste p par la syntaxe p[k]
# le premier rang étant le rang 0
p1[0]
p1[1]
p1[2]

# ca tombe bien pour les polynômes: p[k] donne le coefficient de X^k dans p

# mais on peut désirer connaître le coefficient de p pour un degré donné sans connaître le degré de p, il faut donc écrire une fonction qui calcule cela

def coef(p,k):
  if k<len(p): return p[k]
  else: return 0

# calculons le degré d'un polynôme: c'est le plus grand degré tel que le coefficient correspondant est non nul, et il est borné par la longueur de la liste qui représente p

def deg(p):
  d=0
  # l'instruction suivante est une boucle for:
  # elle exécute les instructions qui la suivent et qui sont décalées
  # par rapport à elle,
  # ceci pour chaque valeur de k dans la liste qui est donnée
  # ici c'est range(len(p))
  for k in range(len(p)):
    if p[k]<>0: d=k # cette instruction est décalée par rapport à
                    # l'instruction for:
                    # elle est exécutée pour chaque valeur de k
  return d # cette instruction n'est pas décalée par rapport à
           # l'instruction for: elle est exécutée quand la boucle for
           # est terminée

deg(p1)
deg(p2)
deg(p3)

# 2. Addition des polynômes

# pour calculer p+q, on additionne les coefficients de même degré
# cela correspond à additionner les termes de même rang des listes représentant
# les polynômes 

def plus_poly(p,q):
  # la variable res va contenir la liste représentant le polynôme somme
  # de p et q, on va lui ajouter des éléments au fur et à mesure que l'on 
  # va calculer les sommes des coefficients de p et q, degré par degré
  # au début elle est vide:
  res=[]
  # parcourons les deux listes p et q, degré par degré
  # du degré 0 au degré maximum, qui est max(deg(p),deg(q))
  # ne pas oublier le range(n) se termine avec n-1 et pas n
  for k in range(max(deg(p),deg(q))+1):
    res=res+[coef(p,k)+coef(q,k)]
  return res

plus_poly(p1,p3)

# plus concis:
# une expression [f(k) for k in A] va calculer la liste des valeurs de f(k)
# pour chaque k de la liste A

def plus_poly(p,q):
  return [coef(p,k)+coef(q,k) for k in range(max(deg(p),deg(q))+1)]

plus_poly(p1,p3)

# 3. Affichage des polynômes

# voir un polynôme sous sa forme en liste n'est pas très parlant, 
# on va programmer qui affiche un polynôme comme on en a l'habitude en maths

# nous aurons besoin de fonctions d'une des bibliothèques python
import sys

# on définit une fonction qui imprime à l'écran une suite de caractères
# (on dit <<chaîne>> en informatique, sans le retour à la ligne que met 
# la fonction standard print

def imprime_chaine(s):
  sys.stdout.write(s)

# et d'une fonction qui fait demême avec un nombre
# pour cela on convertit le nombre en chaîne avec la fonction str

def imprime_nombre(x):
  imprime_chaine(str(x))

# allons-y

def imprime_poly(p):
  deja=False # pour savoir si on déjà imprimé quelque-chose du polynôme
  for k in range(deg(p)+1): 
    c=coef(p,k)
    if c<>0: # toutes les instructions jusqu'à l'instruction deja=True
             # sont décalées: elles sont donc exécutées si c<>0
             # celles d'après ne le sont plus donc sont exécutée 
             # indépendamment de la valeur de c
      if c>0: 
        if deja: imprime_chaine('+')
      else: imprime_chaine('-')
      c=abs(c)
      if c<>1 or k==0: imprime_nombre(c)
      if k>=1: imprime_chaine('X')
      if k>1: 
        imprime_chaine('^') 
        imprime_nombre(k)   
      deja=True
  # fin de la boucle for, car il n'y a plus de décalage 
  # par rapport à l'instruction for 
  if deja==False: imprime_nombre('0')
  imprime_chaine('\n')

imprime_poly(p1)
imprime_poly(p3)
imprime_poly([])
imprime_poly([0,-1])

# 4. Multiplication

# 4.1. Multiplication par une constante a

def mult_constante(a,p):
  return [a*coef(p,k) for k in range(deg(p)+1)]

# 4.2. Multiplication par un monôme X^d

def mult_monome(p,d):
  return ([0 for k in range(d)]+p)

# 4.2. Mutiplication des polynômes

def mult_poly(p,q):
  res=[]
  for k in range(deg(p)+1):
    res=plus_poly(res,
                  mult_constante(coef(p,k),
                                 mult_monome(q,k)))
  return res

p4=[1,1]
imprime_poly(p4)
imprime_poly(mult_poly(p4,p4))

# 4.4. Puissances d'un polynôme

def puis_poly(p,n):
  if n==0: return [1]
  else: return mult_poly(p,puis_poly(p,n-1))

for n in range(13):
  imprime_poly(puis_poly(p4,n))

imprime_poly(puis_poly(p4,500))

leçon 1: départ, nombres entiers et algorithme d'Euclide

Je travaille dans l'environnement cygwin sous Windows, python (version 2) y est par défaut, et j'édite mes fichiers python avec emacs.
Sinon, python (version 2) s'installe sous windows 7: ici. Lancer IDLE (Python GUI). 

Le fichier python contenant ce qui suit est là.



sh-4.1$ python
Python 2.7.3 (default, Dec 18 2012, 13:50:09) 
[GCC 4.5.3] on cygwin
Type "help", "copyright", "credits" or "license" for more information.
>>> 

# Tout ce qui est après un dièse est considéré par python
# comme un commentaire, donc ignoré

# L'algorithme d'Euclide

# 1. La division euclidienne

# 1.1. Le quotient

# on définit une fonction quotient qui prend deux arguments a et b (1ere ligne)
# puis on teste la condition logique a<b (ligne 2)
# si la condition est vérifiée, alors on exécute ce qui suit les 2 points,
# qui consiste à donner la valeur dans cas de quotient(a,b) (ligne 3)
# si la condition n'est pas vérifiée, on exécute ce qui suit
# le mot-clé else (ligne 4): le résultat est obtenu en calculant
# la fonction quotient pour les arguments a-b et b.
# Il s'agit d'un calcul récursif, comme lorsque l'on définit une
# suite par récurrence: u_n+1 = f(u_n).

# pour exécuter la définition de la fonction qui suit, la copier
# et la coller sur la ligne de commande de python, puis finir par
# un retour chariot (Entrée)

def quotient(a,b):
  if a<b:  return 0
  else: return 1+quotient(a-b,b)

quotient(7,2)

# les entiers de python ne sont pas bornés

quotient(500000000000000000000000000000,21111111111111111111111111111)

quotient(-7,2)

# problème, on a pas traité les nombre négatifs, redéfinissons la fonction

def quotient(a,b):
  if a<0: return - quotient(-a,b)
  elif b<0: return - quotient(a,-b)
  elif a<b: return 0
  else: return 1+quotient(a-b,b)

quotient(7,2)
quotient(-7,2)
quotient(7,-2)
quotient(-7,-2)

# remarquer les tests successifs: 
# if ...:... elif ...:... elif ...:... else:...

# 1.2. Le reste

def reste(a,b):
  return a-b*quotient(a,b)

reste(7,2)
reste(-7,2)
reste(7,-2)
reste(-7,-2)


# cette définition du reste et du quotient pour les nombres négatifs n'est pas la seule possible...

# 2. L'algorithme d'Euclide

# il consiste à diviser a par b, ce qui donne un reste b1,
# s'il est non nul on divise b par b1, ce qui donne un reste b2,
# puis ainsi de suite jusqu'à arriver à un reste nul.
# Le dernier reste non nul est alors le pgcd de a et b.

def pgcd(a,b):
  if b==0: return a
  else: return pgcd(b,reste(a,b))

pgcd(6,4)
pgcd(24,15)
pgcd(24543543543,155435434)

# on peut, en se servant des quotients dans cet algorithme,
# calculer les coefficients de Bezout u et v tels que
# u a + v b = pgcd(a,b)
# le resultat de cette fonction est une liste à deux éléments uv=[u,v]
# on accède au premier par la syntaxe uv[0] et au second par uv[1]

def bezout(a,b):
  if b==0: return [1,0]
  else:
    uv= bezout(b,reste(a,b))
    return [uv[1],uv[0]-uv[1]*quotient(a,b)]

bezout(3,4)
bezout(8,5)    

# 3. Un exemple avec la suite de Fibonacci

# on définit cette suite par
# f_0 = 0 et f_1 = 1, f_n+2 = f_n+1 + f_n
# posons fib(n) = f_n

def fib(n):
  if n==0: return 0
  elif n==1: return 1
  else: return fib(n-1)+fib(n-2)

fib(10)

# le pgcd de f_a et f_b est f_c où c est le pgcd de a et b

pgcd(fib(18),fib(27))
fib(9)

Exercices:
1. programmer une fonction qui calcule la factorielle d'un entier n
2. programmer une fonction qui calcule la suite de Collatz:
si $u_n$ est pair, $u_{n+1} = \cfrac {u_n} 2$, sinon $u_{n+1} = 3 u_n+1$.