graphiques avec Python(x,y) et matplotlib

matplotlib est intégré à Python(x,y), pas besoin de le télécharger.
C'est un ensemble de fonctions qui permettent de tracer des graphiques mathématiques.
La liste des fonctions et leur documentation est là (en anglais...)

1. Un premier essai: tracer la fonction sinus sur $[0,6\pi]$:

on charge les bibliothèques nécessaires:


from math import *
import numpy as numpy
import matplotlib.pyplot as pyplot

une courbe est une suite de points du plan reliés par des segments: s'il y en a beaucoup, on a l'illusion d'une courbe lisse.

on crée d'abord la liste t des abcisses de 100 points régulièrement répartis dans $[0,6\pi]$: 

t = numpy.linspace(0.,6*pi,100)

puis on trace la courbe en donnant la liste des ordonnées correspondant aux abcisses données dans la liste t:

pyplot.plot(t, [sin(x) for x in t],'k')

ensuite on définit les bornes du tracé:

pyplot.axis([0,6*pi,-1.5,1.5])

on trace l'axe des abcisses en noir:

pyplot.axhline(linewidth=1, color='k')

puis on insère la définition de la fonction au point $(2,1)$ du plan:

pyplot.text(2,1, r'$\$$x\mapsto\sin(x)$\$$', color='k')

finalement s'affiche cette fenêtre (si elle n'apparaît pas, c'est peut-être qu'elle se trouve cachée derrière une fenêtre, alors cliquer sur son icône dans la barre des tâches):

on peut enregistrer le graphique sous forme d'une image en cliquant sur l'icône en disquette, cela donne cette image:

Notez la possibilité d'écrire du Latex dans les textes du graphique, la classe!

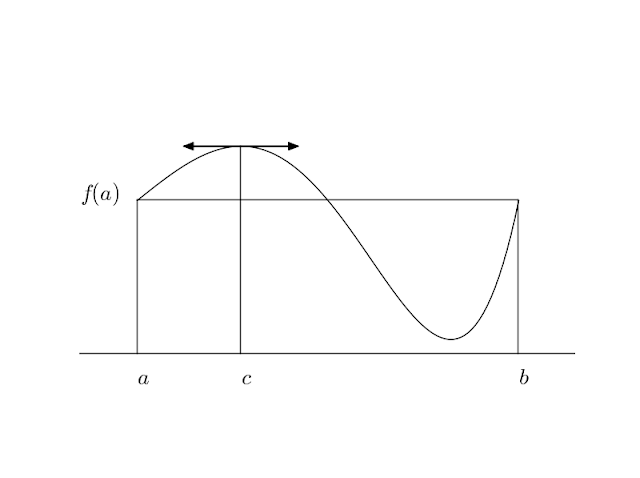
2. Le théorème de Rolle:


# théorème de Rolle
from math import *
import numpy as numpy
import matplotlib.pyplot as pyplot

# les bornes des intervalles
a=0.5
b=2.5
a1=a-0.3
b1=b+0.3
h=4
# la fonction dérivable en question
def f(x):
  y=x-0.5
  return(0.5*(y**5-5*y**3+4*y)+2)

# la courbe de la fonction
t = numpy.linspace(a,b,100)
pyplot.plot(t, [f(x) for x in t],'k')

# le rectangle englobant le tracé
pyplot.axis([a1,b1,-1,h])
pyplot.axis('off') # pour virer le cadre pas très joli
pyplot.plot([a1,b1],[0,0],color='k')
pyplot.plot([a,b],[f(a),f(b)],color='k')
pyplot.plot([a,a],[0,f(a)],color='k')
pyplot.plot([b,b],[0,f(b)],color='k')

c1=.5439122558+0.5 # le point où la dérivée s'annule
pyplot.plot([c1,c1],[0,f(c1)],color='k')

# pour tracer la tangente en (c,f(c)) et ses flèches,
# pas très élégant
pyplot.arrow(c1-0.3,f(c1),2*0.3,0,
  shape='full',head_width=0.1,head_length=.05,fc='k',
  length_includes_head=True)
pyplot.arrow(c1+0.3,f(c1),-2*0.3,0,
  shape='full',head_width=0.1,head_length=.05,fc='k',
  length_includes_head=True)

# enfin les textes du schéma
pyplot.text(a,-0.4, r'$a$', color='k', size=20)
pyplot.text(b,-0.4, r'$b$', color='k', size=20)
pyplot.text(a-0.3,f(a), r'$f(a)$', color='k', size=20)
pyplot.text(c1,-0.4, r'$c$', color='k', size=20)

# sauvegarde le schéma dans un fichier
savefig('rolle.png',format='png')

donne cette image, une fois sauvegardé dans le fichier:

je crois bien que je vais laisser tomber tikz... :)